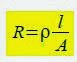Aula 03

RESISTÊNCIA ELÉTRICA (R)

Prof. Jaborandi

1 – Resistência elétrica – Um elétron viajando dentro de um fio encontra resistência ao seu movimento. Suponha um fio ligado a uma bateria conforme a ilustração abaixo. Sabemos que é estabelecida no circuito uma corrente elétrica, devido ao movimento dos elétrons no interior do fio. Nesse movimento ocorrem incontáveis colisões entre os elétrons e os átomos do fio originando uma rota em zigue – zague percorrida pelos elétrons. Chamamos essa dificuldade à passagem dos elétrons pelo fio de resistência elétrica (R).

Assim, dependendo do material do fio, seu comprimento e área da seção reta, ele pode apresentar maior ou menor resistência à passagem da corrente elétrica.

 A resistência elétrica R de um objeto é dada pela seguinte expressão:

R = V / i

V – ddp, voltagem ou tensão no objeto;

i – Corrente elétrica no objeto.

Caminho de um elétron.

 No SI, a unidade de resistência elétrica é o OHM (Ώ). Ώ é uma letra grega denominada ÔMEGA. Assim, quanto maior o valor de R, maior será a oposição que um objeto faz à passagem de corrente elétrica.

Georg Simon Ohm – Físico Alemão. Em 1827 publicou o resultado do seu trabalho mais importante em um folheto : “ O Circuito Galvânico examinado matematicamente” no qual era apresentada a lei sobre a resistência dos condutores, que mais tarde foi chamada de Lei de Ohm. Entre 1826 e 1827, Ohm desenvolveu a primeira teoria matemática da condução elétrica nos circuitos, baseando-se no estudo da condução do calor de Fourier e fabricando os fios metálicos de diferentes comprimentos e diâmetros usados nos seus estudos da condução eléctrica. Este seu trabalho não recebeu o merecido reconhecimento na sua época, tendo a famosa lei de Ohm permanecido desconhecida até 1841 quando recebeu a medalha Copley da Royal britânica.

Exemplos.

a – Uma lâmpada é ligada à tomada de uma residência e verificou-se que uma voltagem de 220 V era aplicada às extremidades dos filamentos da lâmpada. Observou-se então, que uma corrente de 2 A passava pelo filamento. Determine a resistência elétrica da lâmpada.

V = 220 V R = V / i = 220 / 2 = 110 Ώ

i = 2 A

R = ?

b – Se a lâmpada do exercício anterior for ligada a uma bateria de automóvel de 11 V, qual será o valor da corrente elétrica que passará pela lâmpada?

R – 110 Ώ; V = 11 V; i = ?

i = V / R = 11 / 110 = 0,1 A

c – Quando a lâmpada é ligada a outra bateria, verifica-se que uma corrente de 0,5 A atravessa a lâmpada. Qual a voltagem que a bateria está aplicando à lâmpada?

R = 110 Ώ; i = 0,5 A; V = ?

V = R . i = 110 . 0,5 = 55 V

Alguns fatores influenciam o valor da resistência elétrica:

I – A seção reta de um fio, ou seja quanto maior a seção reta (mais grosso) de um fio, menor será a sua resistência elétrica. Observe na ilustração ao lado que ao se aumentar (dobrar) a seção reta do fio (a grossura dele), a resistência caiu para a metade.

II – O comprimento do fio, ou seja, na ilustração ao lado temos dois fios do mesmo material e com mesma seção reta, porém aumentando o comprimento do fio,

 

Fios de material diferente.

III – Material do fio – Se o fio possuir mesma seção reta e comprimento, mas forem de materiais diferentes, o valor da resistência elétrica irá depender do tipo de material do fio, isto é, alguns materiais apresentam maior resistência elétrica do que outros.

Por exemplo, a resistência elétrica do ouro é menor do que a resistência elétrica do ferro.

2 – Resitividade (ρ) – A resistividade (ρ) de um material nos indica a capacidade que ele possui de resistir a corrente elétrica. Assim quanto maior a sua resistividade, maior será a sua resistência. Dessa forma, materiais que possuem baixa resistividade são condutores (metais) de corrente elétrica, enquanto que os que têm alta resistividade são maus condutores de corrente elétrica ou materiais isolantes (a borracha).

seçaõ reta A e comprimento l.

A resistividade de um fio pode ser determinada através da seguinte expressão:

onde:

R – resistência do fio;

l – comprimento do fio;

A – área da seção reta do fio;

ρ – resistividade do material do fio.

No SI, a unidade de resistividade é o ohm . metro ( Ώ . m).

A tabela abaixo ilustra na primeira coluna o valor da resistividade de alguns materiais:

Tabela de resistividade

Exemplo:

Em uma instalação elétrica domiciliar foram gastos 50 m de fios de cobre, cuja seção reta é de 2,5 x 10^-6 m². Calcule a resistência elétrica da fiação.

Solução:

R = ?; l = 50 m; A =2,5 x 10^-6 m²

3 – Resistor. Quando um condutor (uma lâmpada, por exemplo) apresenta uma resistência elétrica, ele é chamado de RESISTOR, mas também pode ser denominado RESISTÊNCIA ELÉTRICA.

Em um diagrama de circuito elétrico, a resistência é representada por uma linha quebrada:

Obs: Consideramos os fios de um circuito com 

R = 0.

 Em situações práticas de eletrônica, por exemplo, os resistores servem para resistir a energia criada pela corrente elétrica. Por exemplo, você tem um componente eletrônico que funciona com três volts. Mas dentro do circuito a energia é maior do que três volts. Se você ligar direto o componente, a peça vai queimar. É neste momento que entra a função do resistor. Você pega um, dois, três, quatro, quantos forem suficiente para diminuir a corrente elétrica, até que haja resistência suficiente para reduzir a corrente elétrica para os três volts do equipamento.

Nesta imagem abaixo você pode ver a imagem de um resistor conectado a um LED. A função do resistor, é RESISTIR à quantidade de corrente em excesso, e só permitir passar a quantidade necessária para o LED ACENDER e não queimar.

Entendeu? Tá vendo ali, na imagem, o resistor? Pois então, é ele quem impede de o LED não queimar.

3.1 – Efeito Joule – Quando os elétrons passam por um resistor, ocorrem colisões entre eles e com os átomos do resistor. Estas colisões geram calor e ocorre o aquecimento do resistor. Este aquecimento é a dissipação da energia elétrica em energia térmica, chamada de Efeito Joule.

Podemos observar o Efeito Joule em:

• Chuveiros elétricos;
• Ferros de passar;
• Chapinha dos cabelos;
• Fogão elétrico;
• Soldadores de componentes eletrônicos, etc.

 No exemplo ao lado temos uma aplicação do Efeito Joule em um fogão elétrico. O alimento é aquecido através de um resistor que dissipa a energia elétrica em energia térmica, gerando assim o calor necessário para o cozimento.

 Às vezes o efeito Joule é prejudicial como é o caso do aquecimento dos processadores de computadores, isolamento de comopnentes de refrigeração, dentre outros.

James Prescott Joule (1818 - 1889) – Física inglès, estudou o comportamento termodinâmico dos gases e o efeito térmico da corrente elétrica, conhecido como Efeito Joule. Este efeito consiste no aquecimento de um condutor quando percorrido por corrente elétrica. Os elétrons livres, que constituem a corrente elétrica, colidem com os átomos do condutor. Em virtude das colisões os átomos passam a vibrar mais intensamente e, em conseqüência, ocorre elevação da temperatura.

 No comércio, os resistores têm a seguinte aparência, na qual o valor da resistência vem expresso em faixas coloridas:

• Primeira faixa: primeiro algarismo do valor da resistência;
• Segunda faixa: segundo algarismo do valor da resistência;
• Terceira faixa: É o expoente da potência de 10 que deve multiplicar os dois algarismos obtidos anteriormente;
• Quarta faixa: Na cor prateada ou dourada é a imprecisão ou tolerância do valor da resistência.

 Assim, para o R1 (resistor 1 da figura acima temos:

• Primeira faixa: verde = 5;
• Segunda faixa: preto = 0;
• Terceira faixa: vermelho = 2;
• Quarta faixa: ouro = 5 %

Então o valor de R1 = 50 x 10² , 5% logo R1 = 5000 Ώ, 5% de tolerância.

Exercícios (consulte a tabela acima de resistividade para resolver os problemas)

1. Calcule a resistência elétrica de um fio de cobre utilizado em instalações domiciliares, de 60 m de comprimento e 3,0 mm² de área de seção transversal. A resistividade do cobre é igual a 1,7 x 10^-8 Ώ . m. Resp: 0,34 Ώ
2. Calcule a resistência elétrica de um fio de alumínio de 20 m de comprimento e 2,0 mm² de área de seção reta. Resp: 0,282 Ώ
3. Calcule a resistência elétrica de um fio de ferro de 100 m de comprimento e 2,5 mm² de área de seção transversal. Resp: 4,0 Ώ
4. Um resistor de resistência elétrica R igual a 10 Ω é percorrido por uma intensidade de corrente elétrica i equivalente a 5 A. Qual é o valor da tensão V no resistor? Resp: 50 V.
5. Um resistor de resistência elétrica R igual a 10 Ω é submetido à ddp (V) de 30 V. Determine a corrente elétrica i que passa pelo resistor. Resp: 3,0 A.
6. Na ilustração 4, a ddp (V) que deve percorrer o resistor R é de 3,0 V. Qual deve ser o valor da resistência elétrica do resistor , se a corrente elétrica que passa por ele é de 5 A? Resp: 0,6 A
7. Determine o valor de R2 utilizando o código de faixas, no exemplo acima. Resp: 250 Ώ, 5% de tolerância.

Acesse o link para estudar Física usando o seu celular:

http://www.youtube.com/watch?v=QVl-GJpRtLg

FIM

Corrente elétrica - Aula 02

1 – Pilha Seca.

A pilha seca é um dispositivo que através de reações químicas que ocorrem em seu interior, é capaz de gerar energia suficiente para criar uma corrente elétrica.

Na ilustração abaixo, podemos ver pilhas secas comuns que encontramos a venda no mercado, bares, lojas de material elétrico, etc.

Pilha comum

Vejamos como seria basicamente o interior de uma pilha seca comum:

Em seu interior temos:

• Polo negativo feito de zinco (Zn);
• Polo positivo, uma barra de grafite;
• No interior, uma pasta de óxido de manganês (MnO₂) e carvão em pó.

Assim as reações químicas resultantes desses elementos no interior da pilha fornecem energia suficiente para gerar uma corrente elétrica.

2 – Associação de pilhas.

Geralmente a pilha seca fornece uma ddp ou voltagem de 1,5 V (1,5 volts, onde volt é a unidade de ddp).

Muitos aparelhos elétricos como lanternas, rádios, controles de TV funcionam com uma ddp superior a 1,5 V para funcionarem, dessa forma precisamos associar (juntar) as pilhas de tal maneira que os aparelhos funcionem.

Na figura abaixo, temos a representação de alguns componentes que aprecem em circuitos elétricos. Repare no desenho que represneta a pilha, onde o traço mais grosso representa o polo negativo da pilha e o mais fino, o polo positivo.

3 – Associação em série de pilhas

A figura abaixo mostra como devemos associar em série um conjunto de pilhas:

Lanterna com suas pilhas associadas em série.

Repare que cada polo positivo está conectado ao polo negativo da pilha seguinte. Desta forma, obtém-se uma associação em série, aonde as ddps de cada pilha são somadas.

Veja na ilustração abaixo como vamos associando as pilhas:

• Associando duas pilhas de 1,5 V, temos 1,5 V + 1,5 V = 3,0 V.
• Associando três pilhas de 1,5 V: 1,5 + 1,5 + 1,5 = 4,5 V

Diagrama de associação em série de pilhas.

Aqui temos Vad = 1,5 V + 1,5 V = 3,0 V

_Vad – É a ddp ou voltagem entre os pontos a e d.

Note que entre a e b, a ddp é Vab = 1,5 V. Ou seja do polo a até o polo b, a ddp é aumentada para 1,5 V.

O polo positivo da pilha 1 (ponto b) tem ddp Vb = 1,5 V. Além do mais, o polo b está conectado ao polo negativo da pilha 2 (ponto c), logo os pontos b e c terão a mesma ddp: Vc = 1,5 V. Do ponto c até o ponto d, a ddp é aumentada de 1,5 V, ou seja passa para 3,0 V e a ddp no ponto d é Vd = 3,0 V

Associação em série de pilhas.

4 - Exercícos

Sendo as pilhas de 1,5 V, calcule V_AB, V_AC e V_AD.

Obs: Muitas pessoas acham que os aparelhos elétricos consomem a intensidade da corrente elétrica (i). Isso não é verdade; o que é consumido é a energia da corrente elétrica. A intensidade i é sempre a mesma em qualquer ponto do circuito elétrico.

Vamos assistir ao vídeo e observar uma prática de associação em paralelo.

FIM

Corrente Elétrica Aula 01

1 – Corrente elétrica (i)

Todas as substâncias possuem átomos e elétrons. Os elétrons estão sempre em movimento e dependendo do elemento químico, estes elétrons movimentam-se de forma livre ou não. A partir dessa propriedade, surge o conceito de corrente elétrica.

A corrente elétrica é o movimento ordenado de elétrons dentro de um objeto, por exemplo, em um fio metálico comum.

Corrente Elétrica

Para que exista uma corrente elétrica devemos ter:

·         Um percurso por onde os elétrons se movimentam (fio metálico);

·         A existência de uma ddp (diferença de potencial) que crie o movimento ordenado de elétrons. (pilha, por exemplo).

Sentido da corrente elétrica

2 – Sentido da corrente elétrica.

Em um circuito elétrico, o sentido de movimento da corrente elétrica será sempre do polo positivo do gerador de corrente elétrica (pilha) para o polo negativo ou o sentido contrário ao do movimento dos elétrons.

Obs:

1.      Pilha – É chamada de gerador elétrico, pois está gerando a ddp que movimenta os elétrons de forma ordenada;

2.      Fio – É chamado de condutor, pois é ele quem conduz os elétrons.

Fio elétrico

3 –  Carga elétrica (Q).

A carga elétrica é dada pela expressão:

Q = n . e

Q = carga elétrica;

n = número de elétrons que passam pela seção reta de um fio;

e = carga do elétron, isto é, e = 1,6 x 10^-19 C.

Obs: A carga do elétron terá sempre o valor de 1,6 x 10^-19 C. 

No SI, a unidade de carga elétrica é o Coulomb ( C ). Mas na prática encontramos o:

·         mC = 10^-3 C (milicoulomb);

·         μC = 10^-6 C (microcoulomb)

Exemplo:

Observe a figura abaixo:

Vemos que pela seção reta do fio estão passando 5 elétrons, então n = 5, então aplicando a fórmula da carga elétrica:

Q = n . e = 5 x 1,6 x 10^-19 = 8,0 x 10^-19 C

Logo a carga elétrica no fio é de 8,0 x 10^-19 C.

4 – Intensidade de corrente elétrica (i).

A intensidade de corrente elétrica é dada pela seguinte expressão:

i = Q / Δ t

i – valor da corrente elétrica;

Q – carga elétrica no fio;

Δ t – tempo que os elétrons levam para atravessar a seção reta do fio.

Exemplo:

Vamos supor que os elétrons do exemplo acima demorem 4,0 x 10^-20 s para atravessar a seção reta do fio. Então Δ t = 4,0 x 10^-19 s. Aplicando a fórmula da corrente elétrica:

i = Q / Δ t = 8,0 x 10^-19 / 4,0 x 10⁺²⁰ = 2,0 x 10 = 20,0 A

Logo, a corrente elétrica que passa pelo fio vale 20 A.

Obs: No SI, a unidade de corrente elétrica é o ampére (A), contudo podem aparecer o:

·         mA = 10^-3 A (miliampére)

·         μA = 10^-6 A (microampére)

Para entender melhor os conceitos vamos assistir ao vídeo abaixo.