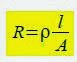Associação de resistores em paralelo

Associação de resistores em paralelo

Na associação em paralelo, a voltagem em cada resistor é a mesma. Repare que a corrente que sai da bateria vai se dividindo em cada nó e dessa forma, cada resistor vai sendo percorrido por uma parte da corrente inicial..

Podemos estabelecer as seguintes equações para as correntes que percorrem o circuito de ressitores em paralelo da ilustração ao lado:

i = i₁ + i₂ + i₃

E para as voltagens em cada resistor:

U = R₁ . i₁

U = R₂ . i₂

U = R₃ . i₃

repare que U = U₁ = U₂ = U₃, pois na associação em paralelo os resistores têm sempre a mesma voltagem.

Podemos determinar a resistência equivalente (Re) da associação em paralelo através da seguinte expressão:

  

Re

Por exemplo:

Vamos supor que R₁ = 2 Ω; R₂ = 3 Ω; U = 12 V no circuito da figura ao lado.

Determine:

a) A resitência equivalente;

b) A corrente elérica em cada resistor.

c) O valor da corrente i.

a) Cálculo da Re:

1/Re = 1/R₁ + 1/R₂

1/Re = 1/2 + 1/3

Re = 6/5 = 1.2 Ω

b) Cálculo da corrente em cada resistor:

Aplicando a lei de Ohm: i = U/R e que U = 12 V é a mesma nos resistores:

i₁ = U/R₁ = 12 / 2 = 6 A

i₂ = U/R₂ = 12 / 3 = 4 A

c) Cálculo da corrente i:

i = i₁ + i₂

i = 6 + 4 = 10 A

Podemos também usar os valores da resistência equivalente:

i = U / Re

i = 12 / 1.2 = 10 A

Vamos assitir ao vídeo abaixo 

FIM

Associação de Resistores

Em um circuito é possível organizar conjuntos de resistores interligados, chamada associação de resistores. O comportamento desta associação varia conforme a ligação entre os resistores, sendo seus possíveis tipos:

1. em série,
2. em paralelo;
3. mista.

Associação em série

Nela, os resitores são dispostos em 'fila', 'um atrás do outro'. Na associação em série, a corrente elétrica que percorre as resitências tem sempre o mesmo valor.

Lâmpadas em série

Resistências em série. 

No entanto a tensão em cada resistor será diferente e nesse caso será dada pela aplicação da primeira lei de Ohm:

U₁ = R₁ . i

U₂ = R₂ . i

U₃ = R₃ . i

U₄ = R₄ . i

Observe que a corrente i é sempre a mesma em cada resistência.

Por exemplo, vamos supor que R₁ = 1 Ω; R₂ = 2 Ω; R₄ = 3 Ω e R₄ = 4 Ω; sendo percorridas por uma corrente de 3 A. Então a voltagem em cada resitência será:

U₁ = 1 . 3 = 3 V

U₂ = 2 . 3 = 6 V

U₃ = 3 . 3 = 9 V

U₄ = 4 . 3 = 12 V

Cálculo da resistência equivalente (R_e)

Na associação em série podemos sibstituir todas as resitências por uma única resitência, denominada resitência equivalente. Então:

R_e = R₁ + R₂ + R₃ + R₄

Então, no exemplo acima, a resistência equivalente será igual a:

R_e = 1 + 2 + 3 + 4 = 10 Ω

Re = 10 Ω

Assim, podemos substituir as quatro residências acima por uma única resitência de 10 Ω, percorrida pela mesma corrente de 3 A, cuja tensão é dada por:

U = R . i = 10 . 3 = 30 V

Note que a tensão de 30 V é a soma das tensões obtidas em cada resitor:

U = 3 + 6 + 9 + 12 = 30 V

vamos relembrar os conceitos no vídeo a seguit:

FIM

Potência elétrica II

Potência em dispositivos elétricos

Podemos dizer que a função básica de uma máquina, elétrica ou não, é transformar energia. Na eletricidade, os dispositivos elétricos estão constantemente transformando energia: o gerador de eletricidade transforma energia não elétrica em energia elétrica, o resistor transforma energia elétrica em calor, etc.

Esta potência é dada pela seguinte expressão:

P = U . i

P – potência elétrica em watts (w);

U – voltagem, tensão elétrica ou ddp em volts (V);

i – corrente elétrica em amperes (A).

Por exemplo: Determine a potência elétrica de um liquidificador ligado a uma tensão de 200 V e é percorrido por uma corrente elétrica de 2 A.

Solução:

U = 200 V; i = 2 A

P = U . i

p = 200 . 2 = 400 W

Logo o liquidificador tem uma potência de 200 W

EFEITO JOULE

Quando a corrente elétrica percorre um condutor como, por exemplo, um metal, faz com que esse se aqueça, transformando, dessa forma, a energia elétrica em energia térmica. Esse fenômeno de conversão de energia nos condutores, foi estudado e descoberto no século XIX pelo cientista e físico britânico James P. Joule. É em homenagem a ele que esse efeito tem o seu nome, efeito joule.

Esse fenômeno tem larga utilização no cotidiano como, por exemplo, em equipamentos de aquecimento como o ferro elétrico, o chuveiro elétrico, a prancha alisadora, o forno elétrico, etc. todos esses equipamentos são compostos, basicamente, por uma resistência que quando percorrida pela corrente elétrica é aquecida, transformando energia elétrica em térmica, ou seja, calor. Outra aplicação prática do efeito joule no cotidiano está nas lâmpadas incandescentes. Criada no século XIX pelo inventor Thomas Edison, ela possui em seu interior um filamento de tungstênio, um metal com ponto de fusão muito elevado, que ao ser percorrido pela corrente elétrica se aquece, podendo chegar a temperaturas de 2500 °C, tornado-se incandescentes e emitindo luz.

Na construção de fusíveis o efeito joule também é aplicado. Fusíveis são dispositivos constituídos por um filamento metálico de baixo ponto de fusão. Dessa forma, quando a corrente elétrica que passa pelo fusível ultrapassa um determinado valor, o calor que é originado pelo efeito joule provoca a fusão do filamento, interrompendo a corrente elétrica. Eles são utilizados como limitadores de corrente elétrica que passa em um circuito elétrico. São encontrados em veículos automotivos, residências, aparelhos elétricos, etc.

Através do efeito Joule é possível determinar a potência elétrica de um aparelho. Ela é dada pela expressão:

P = R . i²

P – potência elétrica em watts (W);

R – resistência em ohms (Ω);

i – corrente elétrica em amperes (A).

Por exemplo: Calcule a potência elétrica gerada por um ferro de passar roupas que possui uma resistência de 200 Ω e é percorrido por uma corrente elétrica de 2 A.

Solução:

R = 200 Ω; i = 2 A

P = R . i²

P = 200 . 2²

P = 200 . 4 = 800 W

Logo o ferro tem uma potência de 800 W de efeito Joule

Vamos assistir ao vídeo sobre efeito Joule

FIM

Potência elétrica I

POTÊNCIA ELÉTRICA

Muitas vezes, na propaganda de certos produtos de eletrônicos, destaca-se a sua potência. Podemos citar como exemplos os aparelhos de som, os chuveiros e as fontes dos microcomputadores.

Sabemos que esses aparelhos necessitam de energia elétrica para funcionar. Ao receberem essa energia elétrica, eles a transformam em outra forma de energia. No caso do chuveiro elétrico, por exemplo, a energia elétrica é transformada em energia térmica, na lâmpada comum a energia elétrica é transformada em energia luminosa e térmica, no ferro de passar roupas, em energia térmica, etc.

Quanto mais energia for transformada em um menor intervalo de tempo, maior será a potência do aparelho. Portanto, podemos concluir que potência elétrica é uma grandeza que mede a rapidez com que a energia elétrica é transformada em outra forma de energia.

Define-se potência elétrica como a razão entre a energia elétrica transformada e o intervalo de tempo dessa transformação. 
 

P = E_el / Δt

P – potência elétrica;

E_el – energia elétrica consumida ou transformada;

Δt – intervalo de tempo de consumo ou transformação da energia.

Unidades de Potência e Energia Elétrica.

Nos livros didáticos em geral, são adotados dois sistemas de unidades, o Sistema Internacional e o sistema prático. Vamos ver as unidades de potência e energia elétrica nesses dois sistemas.

a) Potência Elétrica.

As duas unidades de potência mais usadas são o watt (W) e o quilowatt (kW), onde watt é J / s (Joule dividido por segundo). Elas estão representadas no quadro abaixo, assim como a conversão entre elas: 

 

b) Energia elétrica

No Sistema Internacional, a unidade de energia elétrica é o joule (J), mas na prática usamos o quilowatt hora (kWh). A conta de consumo de eletricidade da sua residência vem nessa unidade. Observe a figura a seguir:

 

Note que o kWh é uma unidade de medida grande e por isso ela é compatível para o uso nas medidas de energia elétrica. Imagine que sem avisar a companhia de fornecimento de energia elétrica resolvesse enviar a conta de luz em joules. O valor da energia consumida seria o valor em kWh multiplicado por 3.600.000J. O resultado seria um valor muito grande que no mínimo resultaria em um susto no dono da conta. 

Cálculo do consumo da energia elétrica.

Vamos por meio de um exemplo bem simples ver como é feito o cálculo do consumo de energia elétrica. Considere um banho de 10 minutos em um chuveiro elétrico de potência de 5.200W. Primeiro, devemos passar a potência do chuveiro para kW e o tempo do banho para horas.

Solução:

P = 5200 W / 1000 = 5,2 KW

Δt = 10 / 60 = 1/6 h

E_el = P . Δt = 5,2 . 1/6 = 0,87 Kwh

Se soubermos o valor do kWh cobrado pela concessionária, poderemos determinar qual foi o custo desse banho. Vamos tomar o preço cobrado pela COELCE que fornece energia na minha casa, que vale R$ 0,30, e vamos multiplicar esse valor pelo valor da energia consumida durante o banho, nesse caso, 0,87kWh.

C = 0,87 . 0,30 = R$ 0,261

Um valor relativamente pequeno. Vamos considerar uma família de 4 pessoas, então o custo diário será (se elas tomarem banho apenas 1 vez por dia):

 

C = 4 . 0,261 = R$ 1,044

Agora vamos considerar esse consumo para 1 mês de 30 dias:

C = 30 . 1,044 = R$ 31,32

Então podemos concluir que o chuveiro realmente é responsável por uma fatia significativa na despesa mensal com a conta de luz. 

 Vamos assistir à primeira parte desse vídeo sobre o calculo do consumo de energia:
 

FIM

 

Aula 04

RESISTOR ÔHMICO

Vamos observar a tabela abaixo que representa o comportamento de um resistor:

V (V)	1	2	3	4
i (A)	0,1	0,2	0,3	0,4

Vamos também desenhar o gráfico:

Observe que se dividirmos a voltagem (V) pela corrente, obtemos sempre o mesmo valor:

1 / 0,1 = 2 / 0,2 = 3 / 0,3 = 4 / 0,4 = 10

Mas lembrando que R = V / i, então podemos dizer que a resistência do resistor acima é constante, ou seja, é sempre a mesma e igual a 10 Ώ. Observe que o gráfico obtido é uma reta.

Os resistores que exibem este comportamento obedecem à Lei de Ohm e são chamados de RESISTORES ÔHMICOS.

Assim, quando um resistor for ôhmico, o seu gráfico será sempre uma linha reta conforme o gráfico da figura abaixo.

Exercícios

1 - Os valores de voltagem e corrente de um resistor estão representados no gráfico abaixo. Diga se ele é um resistor ôhmico e determine a sua resistência.

Cálculos:

2 – O gráfico abaixo ilustra o comportamento de um rsistor ôhmico. A partir dessa informação determine o valor X da corrente e Y da tensão elétrica..

Cálculos:

3 – assinale o gráfico que representa um resistor ôhmico.

Resposta:

4 – A curva característica de um resistor ôhmico está ilustrada na figura abaixo:

Calcule o valor da tensão U e da corrente i no resistor.

5 - Um resistor ôhmico quando submetido a uma ddp de 6 V é percorrido por uma corrente elétrica de intensidade 2 A. Qual é a ddp que deve ser aplicada ao resistor para que a corrente elétrica que o atravesse tenha intensidade 3,2 A?

FIM

Questões ENEM

http://fisicainterativa.com/fisica-enem/questoes-resolvidas/

Aula 03

RESISTÊNCIA ELÉTRICA (R)

Prof. Jaborandi

1 – Resistência elétrica – Um elétron viajando dentro de um fio encontra resistência ao seu movimento. Suponha um fio ligado a uma bateria conforme a ilustração abaixo. Sabemos que é estabelecida no circuito uma corrente elétrica, devido ao movimento dos elétrons no interior do fio. Nesse movimento ocorrem incontáveis colisões entre os elétrons e os átomos do fio originando uma rota em zigue – zague percorrida pelos elétrons. Chamamos essa dificuldade à passagem dos elétrons pelo fio de resistência elétrica (R).

Assim, dependendo do material do fio, seu comprimento e área da seção reta, ele pode apresentar maior ou menor resistência à passagem da corrente elétrica.

 A resistência elétrica R de um objeto é dada pela seguinte expressão:

R = V / i

V – ddp, voltagem ou tensão no objeto;

i – Corrente elétrica no objeto.

Caminho de um elétron.

 No SI, a unidade de resistência elétrica é o OHM (Ώ). Ώ é uma letra grega denominada ÔMEGA. Assim, quanto maior o valor de R, maior será a oposição que um objeto faz à passagem de corrente elétrica.

Georg Simon Ohm – Físico Alemão. Em 1827 publicou o resultado do seu trabalho mais importante em um folheto : “ O Circuito Galvânico examinado matematicamente” no qual era apresentada a lei sobre a resistência dos condutores, que mais tarde foi chamada de Lei de Ohm. Entre 1826 e 1827, Ohm desenvolveu a primeira teoria matemática da condução elétrica nos circuitos, baseando-se no estudo da condução do calor de Fourier e fabricando os fios metálicos de diferentes comprimentos e diâmetros usados nos seus estudos da condução eléctrica. Este seu trabalho não recebeu o merecido reconhecimento na sua época, tendo a famosa lei de Ohm permanecido desconhecida até 1841 quando recebeu a medalha Copley da Royal britânica.

Exemplos.

a – Uma lâmpada é ligada à tomada de uma residência e verificou-se que uma voltagem de 220 V era aplicada às extremidades dos filamentos da lâmpada. Observou-se então, que uma corrente de 2 A passava pelo filamento. Determine a resistência elétrica da lâmpada.

V = 220 V R = V / i = 220 / 2 = 110 Ώ

i = 2 A

R = ?

b – Se a lâmpada do exercício anterior for ligada a uma bateria de automóvel de 11 V, qual será o valor da corrente elétrica que passará pela lâmpada?

R – 110 Ώ; V = 11 V; i = ?

i = V / R = 11 / 110 = 0,1 A

c – Quando a lâmpada é ligada a outra bateria, verifica-se que uma corrente de 0,5 A atravessa a lâmpada. Qual a voltagem que a bateria está aplicando à lâmpada?

R = 110 Ώ; i = 0,5 A; V = ?

V = R . i = 110 . 0,5 = 55 V

Alguns fatores influenciam o valor da resistência elétrica:

I – A seção reta de um fio, ou seja quanto maior a seção reta (mais grosso) de um fio, menor será a sua resistência elétrica. Observe na ilustração ao lado que ao se aumentar (dobrar) a seção reta do fio (a grossura dele), a resistência caiu para a metade.

II – O comprimento do fio, ou seja, na ilustração ao lado temos dois fios do mesmo material e com mesma seção reta, porém aumentando o comprimento do fio,

 

Fios de material diferente.

III – Material do fio – Se o fio possuir mesma seção reta e comprimento, mas forem de materiais diferentes, o valor da resistência elétrica irá depender do tipo de material do fio, isto é, alguns materiais apresentam maior resistência elétrica do que outros.

Por exemplo, a resistência elétrica do ouro é menor do que a resistência elétrica do ferro.

2 – Resitividade (ρ) – A resistividade (ρ) de um material nos indica a capacidade que ele possui de resistir a corrente elétrica. Assim quanto maior a sua resistividade, maior será a sua resistência. Dessa forma, materiais que possuem baixa resistividade são condutores (metais) de corrente elétrica, enquanto que os que têm alta resistividade são maus condutores de corrente elétrica ou materiais isolantes (a borracha).

seçaõ reta A e comprimento l.

A resistividade de um fio pode ser determinada através da seguinte expressão:

onde:

R – resistência do fio;

l – comprimento do fio;

A – área da seção reta do fio;

ρ – resistividade do material do fio.

No SI, a unidade de resistividade é o ohm . metro ( Ώ . m).

A tabela abaixo ilustra na primeira coluna o valor da resistividade de alguns materiais:

Tabela de resistividade

Exemplo:

Em uma instalação elétrica domiciliar foram gastos 50 m de fios de cobre, cuja seção reta é de 2,5 x 10^-6 m². Calcule a resistência elétrica da fiação.

Solução:

R = ?; l = 50 m; A =2,5 x 10^-6 m²

3 – Resistor. Quando um condutor (uma lâmpada, por exemplo) apresenta uma resistência elétrica, ele é chamado de RESISTOR, mas também pode ser denominado RESISTÊNCIA ELÉTRICA.

Em um diagrama de circuito elétrico, a resistência é representada por uma linha quebrada:

Obs: Consideramos os fios de um circuito com 

R = 0.

 Em situações práticas de eletrônica, por exemplo, os resistores servem para resistir a energia criada pela corrente elétrica. Por exemplo, você tem um componente eletrônico que funciona com três volts. Mas dentro do circuito a energia é maior do que três volts. Se você ligar direto o componente, a peça vai queimar. É neste momento que entra a função do resistor. Você pega um, dois, três, quatro, quantos forem suficiente para diminuir a corrente elétrica, até que haja resistência suficiente para reduzir a corrente elétrica para os três volts do equipamento.

Nesta imagem abaixo você pode ver a imagem de um resistor conectado a um LED. A função do resistor, é RESISTIR à quantidade de corrente em excesso, e só permitir passar a quantidade necessária para o LED ACENDER e não queimar.

Entendeu? Tá vendo ali, na imagem, o resistor? Pois então, é ele quem impede de o LED não queimar.

3.1 – Efeito Joule – Quando os elétrons passam por um resistor, ocorrem colisões entre eles e com os átomos do resistor. Estas colisões geram calor e ocorre o aquecimento do resistor. Este aquecimento é a dissipação da energia elétrica em energia térmica, chamada de Efeito Joule.

Podemos observar o Efeito Joule em:

• Chuveiros elétricos;
• Ferros de passar;
• Chapinha dos cabelos;
• Fogão elétrico;
• Soldadores de componentes eletrônicos, etc.

 No exemplo ao lado temos uma aplicação do Efeito Joule em um fogão elétrico. O alimento é aquecido através de um resistor que dissipa a energia elétrica em energia térmica, gerando assim o calor necessário para o cozimento.

 Às vezes o efeito Joule é prejudicial como é o caso do aquecimento dos processadores de computadores, isolamento de comopnentes de refrigeração, dentre outros.

James Prescott Joule (1818 - 1889) – Física inglès, estudou o comportamento termodinâmico dos gases e o efeito térmico da corrente elétrica, conhecido como Efeito Joule. Este efeito consiste no aquecimento de um condutor quando percorrido por corrente elétrica. Os elétrons livres, que constituem a corrente elétrica, colidem com os átomos do condutor. Em virtude das colisões os átomos passam a vibrar mais intensamente e, em conseqüência, ocorre elevação da temperatura.

 No comércio, os resistores têm a seguinte aparência, na qual o valor da resistência vem expresso em faixas coloridas:

• Primeira faixa: primeiro algarismo do valor da resistência;
• Segunda faixa: segundo algarismo do valor da resistência;
• Terceira faixa: É o expoente da potência de 10 que deve multiplicar os dois algarismos obtidos anteriormente;
• Quarta faixa: Na cor prateada ou dourada é a imprecisão ou tolerância do valor da resistência.

 Assim, para o R1 (resistor 1 da figura acima temos:

• Primeira faixa: verde = 5;
• Segunda faixa: preto = 0;
• Terceira faixa: vermelho = 2;
• Quarta faixa: ouro = 5 %

Então o valor de R1 = 50 x 10² , 5% logo R1 = 5000 Ώ, 5% de tolerância.

Exercícios (consulte a tabela acima de resistividade para resolver os problemas)

1. Calcule a resistência elétrica de um fio de cobre utilizado em instalações domiciliares, de 60 m de comprimento e 3,0 mm² de área de seção transversal. A resistividade do cobre é igual a 1,7 x 10^-8 Ώ . m. Resp: 0,34 Ώ
2. Calcule a resistência elétrica de um fio de alumínio de 20 m de comprimento e 2,0 mm² de área de seção reta. Resp: 0,282 Ώ
3. Calcule a resistência elétrica de um fio de ferro de 100 m de comprimento e 2,5 mm² de área de seção transversal. Resp: 4,0 Ώ
4. Um resistor de resistência elétrica R igual a 10 Ω é percorrido por uma intensidade de corrente elétrica i equivalente a 5 A. Qual é o valor da tensão V no resistor? Resp: 50 V.
5. Um resistor de resistência elétrica R igual a 10 Ω é submetido à ddp (V) de 30 V. Determine a corrente elétrica i que passa pelo resistor. Resp: 3,0 A.
6. Na ilustração 4, a ddp (V) que deve percorrer o resistor R é de 3,0 V. Qual deve ser o valor da resistência elétrica do resistor , se a corrente elétrica que passa por ele é de 5 A? Resp: 0,6 A
7. Determine o valor de R2 utilizando o código de faixas, no exemplo acima. Resp: 250 Ώ, 5% de tolerância.

Acesse o link para estudar Física usando o seu celular:

http://www.youtube.com/watch?v=QVl-GJpRtLg

FIM